The Math Profs
|
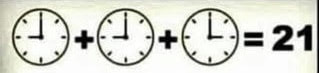
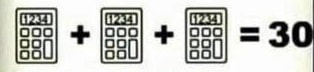
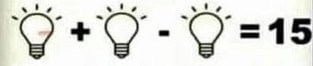
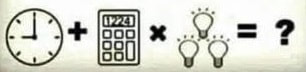
Step 1: Find the value of the clock in Row 4 Note that the clock faces in Row 1 are NOT identical. That's the first mistake people will make, if they're speeding through the puzzle. They'll think the clocks are identical, and thus the sum of the three identical clocks is 21, which gives each clock a value of 7. But since the clocks are not identical, we have to find their value another way. Note that the clock faces are 9, 9, and 3, respectively. Now, what is the sum of \( 9+9+3\) ? Ah-ha!! There's our answer. Each clock has a value equal to the time showing on its face. So the clock in Row 4 is equal to 9. Step 2: Find the value of the calculator in Row 4 If we look at Row 2, we see that this time the objects are identical. Thus, we can say 3 calculators is equal to 30, and therefore 1 calculator is equal to 10. But here we need to be careful, or else we'll make another mistake. To be more precise, we should have said that each of the calculators in Row 2 is equal to 10. You see, the calculator in Row 4 is not the same as the calculators in Row 2. The screen has a different number. So, what do we do? Well, it stands to reason that the value of each calculator is somehow related to its screen number. Does this work for the Row 2 calculators? We found that each Row 2 calculator has a value of 10, and each screen shows 1234. Well, what is the sum of \(1+2+3+4 \) ? Hey! I think we're onto something! If each calculator's value is equal to the sum of the digits showing on its screen, then that calculator in row 4 has a value of \(1+2+2+4=9 \). Step 3: Find the value of the three light bulbs in Row 4. Looking at Row 3, we see that all of the light bulbs are identical. So, on the left-hand side, we're simply starting with 1 light bulb, adding another bulb to it, and then removing the one we just added … which still leaves us with just one light bulb. This means that one light bulb has a value of 15, and therefore the 3 light bulbs in Row 4 are equal to....WAIT!! Did you catch it? I'll admit, I missed it the first time I looked at this problem. The light bulbs in Row 4 are NOT the same as the light bulbs in Row 3. The bulbs in Row 3 each have 5 light rays above each bulb. However, the bulbs in Row 4 each have 4 light rays. What does this mean? Well, it implies that the value of a light bulb somehow depends on the number of light rays above that bulb. We know that each bulb with 5 light rays has a value of 15. To me, this suggests that each light ray contributes a value of 3 to the total bulb value. So, if I want to know the value of a light bulb, I just count up the number of light rays above the bulb and multiply by 3. Since each bulb in Row 4 has 4 light rays, this means that each Row 4 light bulb has a value of \(4 \times 3 = 12\). And therefore, the 3 bulbs in Row 4 are equal to \(3 \times 12 = 36\). (Whew!! Now do you understand why I said this puzzle will test your observational skills, rather than your mathematical abilities?) Step 4: Putting everything together. Okay, substituting for the clock, the calculator, and the 3 light bulbs, Row 4 becomes \(9+10\times36\) Note that the second operation is multiplication, and not addition. (This detail is easily missed by the eyes when glancing from symbol to symbol.) And the Rules for Order of Operations tells us the multiplication is performed first, before the addition. Therefore, Row 4 is given by \(9+360=369\). Afterword: Okay, so 369 is our preferred solution. Now, usually in mathematics we don't speak of a preferred solution. We simply say the solution. But, unfortunately, for a lot of the viral puzzles floating around on social media, the rules are a little....vague. Maybe this helps make puzzles a bit more interesting (we're being generous, here), but it definitely creates some problems. Instead of being able to say "This follows from this, which follows from this, and therefore the answer is this," we are reduced to saying, "I think the best answer is given by this, because I think this is what the puzzle creator intended." Now, I want you to go back to our solution, and look at the assumptions we made. I can see several. For instance, when we noticed that the clock faces in Row 1 were different and also added up to 21, we quickly assumed the puzzle creator intended for clock values to be based on the number shown by the clock face. I think that's a pretty reasonable assumption, don't you? And I think most people would agree. But at the same time, the puzzle creator might have just put different numbers on the faces for variation, and really meant for all clock values to be the same no matter the face value. I doubt it. But it's possible. And that would lead to a different final answer, wouldn't it? But what about the calculator assumption? Once I saw that a calculator screen with 1234 was associated with the value 10, the first thought that occurred to me was "Oh, I just add the screen digits together and that gives the value." But others might have come up with a different scheme. And there really are infinitely many possibilities. I mean, basically you're just looking for a function that takes four input values (the four digits on the screen) and gives one output value. So the function will take the form \(f(x_1, x_2, x_3, x_4)=y \). Now, the only restriction on our creativity in building such a function is that a calculator screen with "1234" on it must have a value of 10. So our function must satisfy \(f(1,2,3,4)=10 \). The function I chose (where I simply summed up the screen digits) could be written as \(f(x_1, x_2, x_3, x_4)=x_1+x_2+x_3+x_4 \). But I can just as easily come up with a different function that still meets our criteria. What about \(g(x_1, x_2, x_3, x_4)=2x_2+2x_3 \)? Does that satisfy our condition? Indeed it does! Check it and you'll see that \(g(1,2,3,4)=2(2)+2(3)=10 \). And that function would yield a different final answer for our puzzle solution, right? In fact, do you realize that if you give me any number in the world, then I can make the puzzle solution equal to that number, simply by creatively choosing the function that evaluates the calculator screens?! And, since the rules are vague, all I would need to do is be willing to argue its defence in an authoritative manner, and I could claim that my solution is the correct solution, and everyone else is wrong - including the puzzle creator, if need be. But rather than go that route, I'd just stick with our preferred solution above, and most folks will agree with you without the need for added argument. Homework: And we can't leave you without some homework!!
If you like our puzzles and explanations, please visit our store and check out our problem-solving and logic puzzle books!
0 Comments
Leave a Reply. |
Archives
February 2021
CategoriesAuthorsBrian and Melanie Fulton both earned doctoral degrees in mathematics at Virginia Tech. They formerly taught math at the university level, and now run a hobby farm while accuracy-checking collegiate mathematics texts. They homeschool their four children, frequently employing the aid of chicken, dairy goat, cat, and dog tutors. |
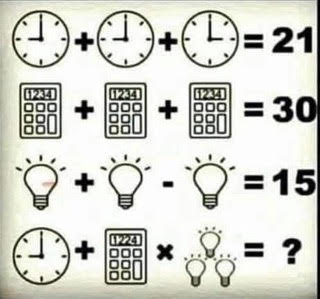
 RSS Feed
RSS Feed
